Post

重新总结激活函数和损失函数

Posted Updated
By li.yaozong
10 min read
重新总结激活函数和损失函数

一、常用损失函数及使用场景

1. 均方误差（MSE, Mean Squared Error）

  • 公式：

    \[L = \frac{1}{n} \sum_{i=1}^n (y_i - \hat{y}_i)^2\]
  • 使用场景：回归任务（如房价预测、温度预测）。
  • 优点：计算简单，梯度平滑，收敛快。
  • 缺点：对异常值敏感，可能导致梯度爆炸。
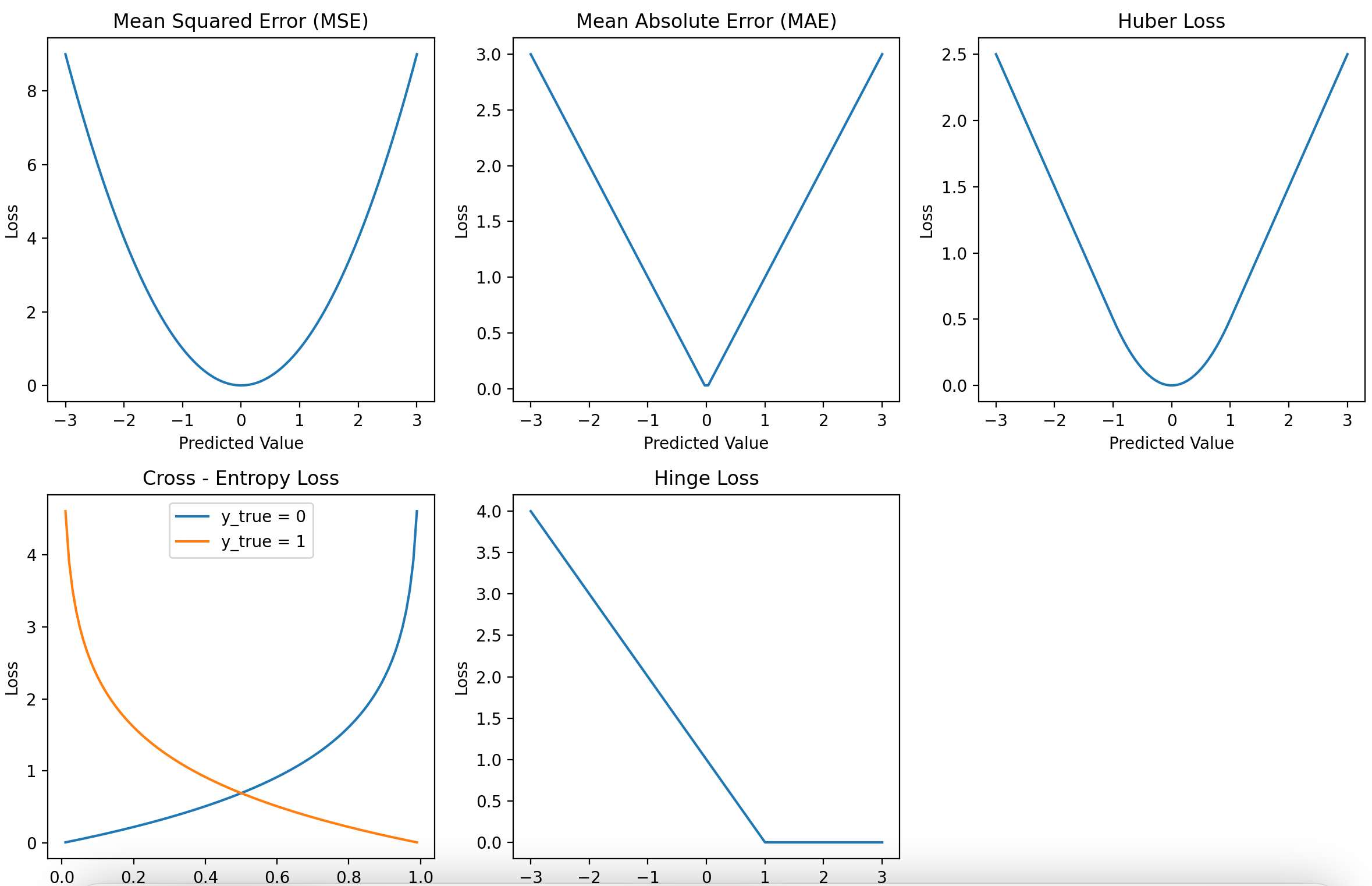
  • 图像特点：二次函数曲线，误差越大损失增长越快。

2. 平均绝对误差（MAE, Mean Absolute Error）

  • 公式：

    \[L = \frac{1}{n} \sum_{i=1}^n |y_i - \hat{y}_i|\]
  • 使用场景：回归任务（对异常值鲁棒的场景，如金融数据预测）。
  • 优点：对异常值鲁棒，梯度稳定。
  • 缺点：收敛速度较慢。
  • 图像特点：线性增长，误差与损失呈正比。

3. Huber损失（Smooth L1 Loss）

  • 公式：

    \[L = \begin{cases} 0.5 (y_i - \hat{y}_i)^2 & \text{if } |y_i - \hat{y}_i| \le \delta \\ \delta (|y_i - \hat{y}_i| - 0.5 \delta) & \text{otherwise} \end{cases}\]
  • 使用场景：回归任务（平衡MSE和MAE的优势，适合含噪声数据）。
  • 优点：结合MSE的平滑梯度和MAE的鲁棒性。
  • 缺点：需手动调整超参数$\delta$。

4. 交叉熵损失（Cross-Entropy Loss）

  • 二分类公式：

    \[L = -\frac{1}{n} \sum_{i=1}^n [y_i \log(\hat{y}_i) + (1 - y_i) \log(1 - \hat{y}_i)]\]

  • 多分类公式：

    \[L = -\frac{1}{n} \sum_{i=1}^n \sum_{c=1}^C y_{i,c} \log(\hat{y}_{i,c})\]
  • 使用场景：分类任务（二分类用Sigmoid+二元交叉熵，多分类用Softmax+交叉熵）。
  • 优点：梯度更新高效，适合概率分布优化。
  • 缺点：对类别不平衡敏感。
  • 图像特点：对数函数曲线，预测偏离真实值时损失急剧上升。

5. Hinge损失（支持向量机损失）

  • 公式：
\[L = \max(0, 1 - y_i \cdot \hat{y}_i)\]
  • 使用场景：二分类任务（如SVM模型）。
  • 优点：生成稀疏解，适合支持向量机。
  • 缺点：仅支持二分类，对噪声敏感。
  • 图像特点：分段线性函数，当预测正确且置信度大于1时损失为0。

二、常用激活函数及使用场景

1. Sigmoid

  • 公式：
\[\sigma(x) = \frac{1}{1 + e^{-x}}\]
  • 使用场景：二分类输出层、概率映射（如逻辑回归）:cite[1]:cite[4]。
  • 优点：输出范围[0,1]，适合概率解释。
  • 缺点：梯度消失问题，输出非零均值。
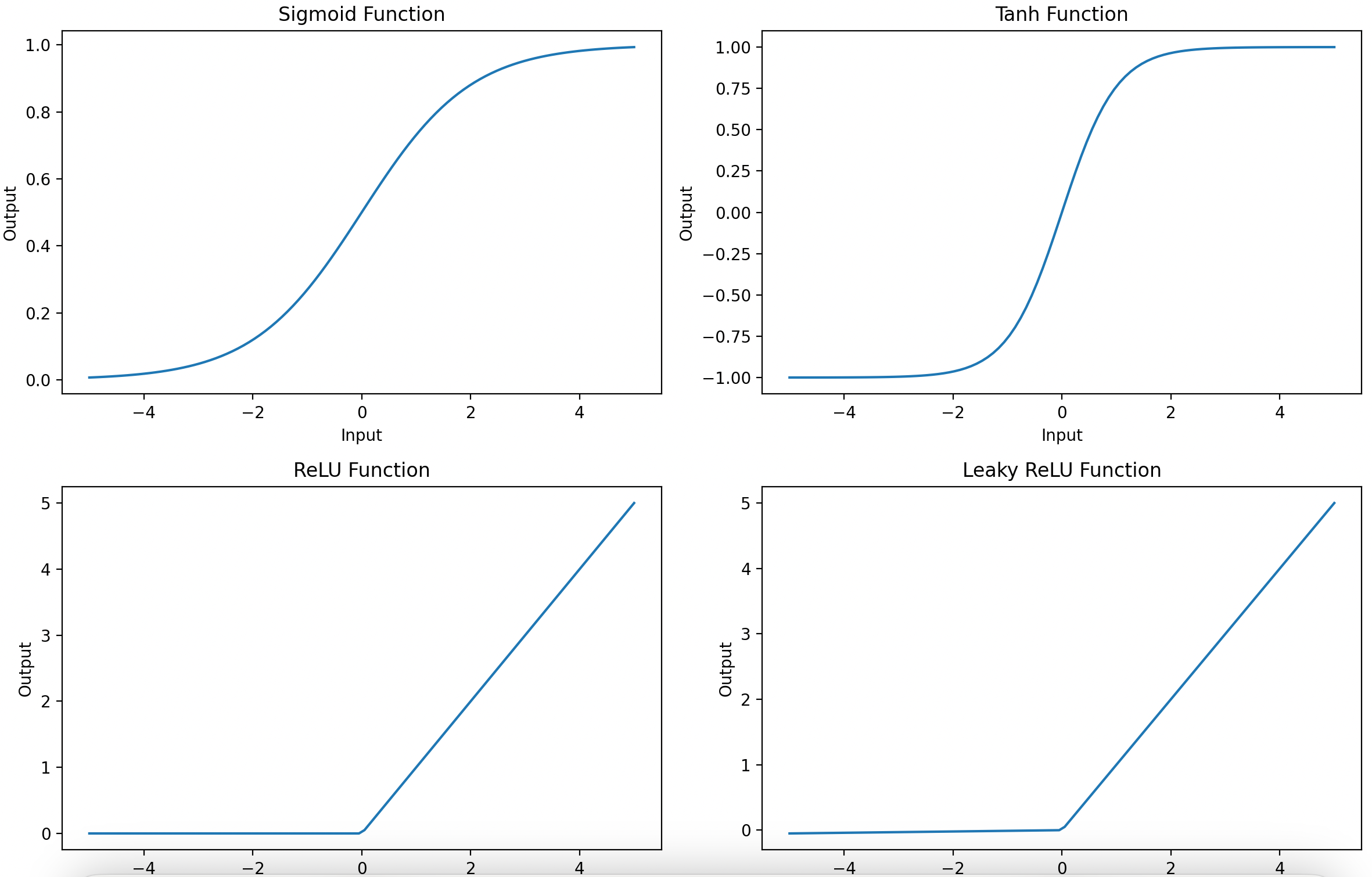
  • 图像特点：S型曲线，两端饱和区梯度趋近于0。

2. Tanh

  • 公式：
\[\tanh(x) = \frac{e^x - e^{-x}}{e^x + e^{-x}}\]
  • 使用场景：隐藏层（比Sigmoid更适合梯度传播）。
  • 优点：输出范围[-1,1]，零均值缓解梯度问题。
  • 缺点：梯度消失问题仍存在。
  • 图像特点：S型曲线，中心对称。

3. ReLU（Rectified Linear Unit）

  • 公式：
\[\text{ReLU}(x) = \max(0, x)\]
  • 使用场景：隐藏层（CNN、全连接网络的默认选择）。
  • 优点：计算高效，缓解梯度消失。
  • 缺点：“死亡神经元”问题（输入为负时梯度为0）。
  • 图像特点：左半轴恒为0，右半轴线性增长。

4. Leaky ReLU

  • 公式：
\[\text{LeakyReLU}(x) = \begin{cases} x & \text{if } x > 0 \\ \alpha x & \text{otherwise} \end{cases}\]
  • 使用场景：改进ReLU的死亡神经元问题（如GANs）。
  • 优点：缓解死亡神经元问题，$\alpha$通常设为0.01。
  • 缺点：需调参选择$\alpha$。

5. Softmax

  • 公式：
\[\text{Softmax}(x_i) = \frac{e^{x_i}}{\sum_{j=1}^C e^{x_j}}\]
  • 使用场景：多分类输出层（如图像分类）。
  • 优点：输出概率分布，总和为1。
  • 缺点：数值不稳定（需配合Log-Sum-Exp技巧）。

三、对比表格

类型函数名称主要场景优点缺点
损失函数MSE回归任务梯度平滑，收敛快对异常值敏感
 MAE鲁棒回归对异常值鲁棒收敛慢
 Huber含噪声的回归平衡MSE和MAE需调参
 交叉熵分类任务高效优化概率分布类别不平衡敏感
 HingeSVM二分类稀疏解，支持最大间隔分类仅支持二分类
激活函数Sigmoid二分类输出层概率解释清晰梯度消失
 Tanh隐藏层零均值，梯度传播更优梯度消失
 ReLU隐藏层（默认选择）计算高效，缓解梯度消失死亡神经元
 Leaky ReLU改进ReLU的隐藏层缓解死亡神经元问题需调参
 Softmax多分类输出层输出概率分布数值不稳定

四、函数图像特征总结

  1. Sigmoid/Tanh：S型曲线，两端梯度趋近于0，易导致梯度消失。
  2. ReLU系列：分段线性函数，正区间梯度恒定，负区间梯度为0（ReLU）或小斜率（Leaky ReLU）。
  3. MSE vs MAE：MSE为抛物线，MAE为V型直线；Huber损失在误差小时为抛物线，大时为直线。
  4. 交叉熵：对数曲线，预测错误时损失急剧上升。

损失函数图像

img.png

激活函数图像

img.png —

GELU（Gaussian Error Linear Unit）激活函数

数学公式

GELU激活函数的定义基于高斯分布的累积分布函数（CDF），其数学表达式为：

\[\text{GELU}(x) = x \cdot \Phi(x)\]

其中，$\Phi(x)$ 是标准正态分布（均值为0，标准差为1）的累积分布函数，即：

\[\Phi(x) = \frac{1}{2} \left( 1 + \text{erf} \left( \frac{x}{\sqrt{2}} \right) \right)\]

为便于计算，常用以下近似公式替代：

\[\text{GELU}(x) \approx 0.5x \left( 1 + \tanh\left( \sqrt{\frac{2}{\pi}} \left( x + 0.044715x^3 \right) \right) \right)\]

提出背景

GELU由Dan Hendrycks和Kevin Gimpel于2016年在论文《Gaussian Error Linear Units (GELUs)》中提出，旨在结合随机正则化的思想设计一种更平滑的激活函数。其核心思想是：

  • 通过输入值的概率分布动态调节神经元激活状态，而非像ReLU一样仅依赖符号。
  • 在训练过程中引入随机性，模拟Dropout等正则化技术的效果。

应用场景

GELU广泛应用于 自然语言处理（NLP） 和 计算机视觉（CV） 中的深度学习模型，尤其适合以下场景：

  1. Transformer架构：如BERT、GPT等预训练模型默认使用GELU。
  2. 深层网络：因其平滑性，缓解梯度消失问题。
  3. 自注意力机制：与多头注意力配合，提升模型表达能力。

优势与劣势

优势

  1. 平滑性：梯度连续，避免ReLU在$x=0$处的梯度突变。
  2. 自适应激活：根据输入分布动态调整激活强度，保留部分负值信息。
  3. 性能优越：在NLP任务中表现优于ReLU、ELU等激活函数。

劣势

  1. 计算成本高：精确计算$\Phi(x)$需误差函数（erf），近似计算依赖复杂运算（如立方项）。
  2. 可解释性弱：相比ReLU，动态激活机制更复杂，难以直观解释。

函数图像

GELU的图像具有以下特点：

  • 形状：类似ReLU，但在负区间平滑过渡（非硬截断）。
  • 对比：与Swish函数$x \cdot \text{sigmoid}(\beta x)$形状相似，但数学形式不同。

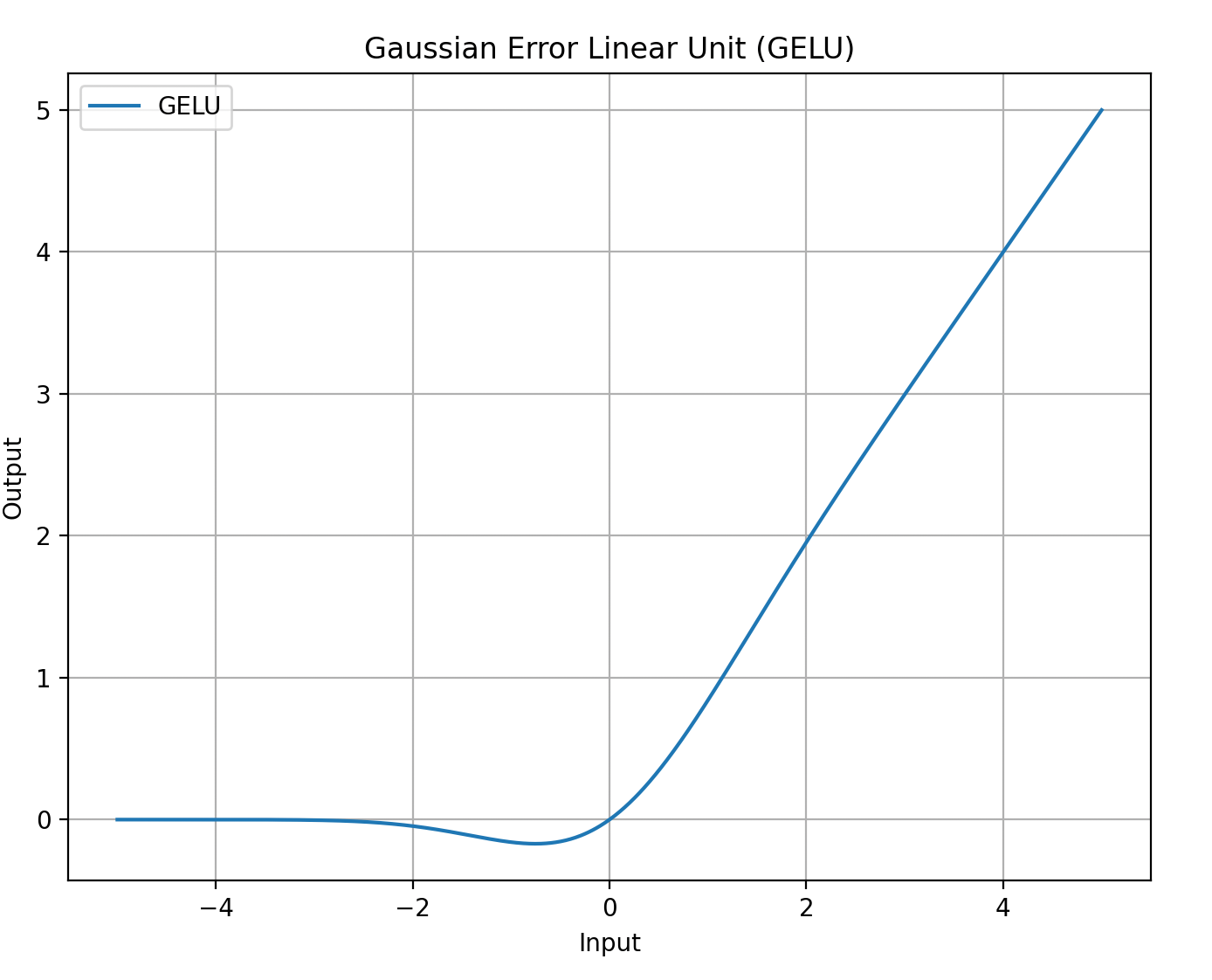img.png （注：图像展示GELU与ReLU、ELU的对比，负区间的平滑性明显。）

总结

GELU通过概率建模实现了更自然的神经元激活机制，在Transformer等复杂模型中表现优异，但需权衡计算效率。其设计思想为激活函数的研究提供了新方向。

机器学习
This post is licensed under CC BY 4.0 by the author.

Trending Tags

大模型